En el solsticio de verano,
los rayos solares inciden perpendicularmente sobre Siena (Asuán). En
Alejandría, más al norte, midiendo la altura de un edificio y la longitud de la
sombra que proyecta, se puede determinar el ángulo formado con el plano de la
eclíptica, en el que se encuentran el Sol y la ciudad de Siena, ángulo que es
precisamente la diferencia de latitud entre ambas ciudades. Conocida ésta,
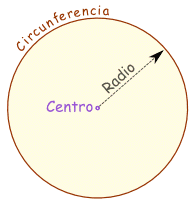
basta medir el arco de circunferencia y extrapolar el resultado a la
circunferencia completa (360º).
Estatua de bronce de
Arquímedes ubicada en el observatorio Archenhold en Berlín. Fue esculpida por
Gerhard Thieme e inaugurada en 1972.
Una esfera tiene 2/3 exactos
del volumen y de la superficie del cilindro que la circunscribe. Una esfera y
un cilindro fueron colocados encima de la tumba de Arquímedes, cumpliendo con
su voluntad.
“¿Quién enseño matemáticas
las abejas?”.
Este hecho fue comprobado
por Papus de Alejandría, matemático griego que vivió del año 284 al 305.
Las abejas, cuando guardan
la miel, tienen que resolver varios problemas. Necesitan guardar la miel en
celdillas individuales, de tal manera que formen un mosaico sin huecos ni
salientes entre las celdillas, ya que hay que aprovechar el espacio al máximo.
Solo podrían hacerlo con
triángulos, cuadrados y hexágonos. ¿Por qué eligieron los hexágonos si son más
difíciles de construir?
La respuesta es un problema
del perímetro. Papus demostró que, entre todos los polígonos regulares con el
mismo perímetro, encierran más área aquellos que tengan mayor número de lados.
Por eso, la figura que encierra área para un perímetro determinado es el
círculo, que posee un número infinito de lados.
Por eso las abejas
construyen sus celdillas de forma hexagonal, ya que, gastando la misma cantidad
de cera en las celdillas, consiguen mayor superficie para guardar su miel.
Y la pregunta es: “¿Quién
les enseñó esto a las abejas?”
Las abejas, en virtud de una
cierta intuición geométrica, saben que el hexágono es mayor que el triángulo y
que el cuadrado y que podrá contener más miel con el mismo número de material.
Yo pensaba que las abejas
eran insectos mucho más sencillos y no conocía mucho de ellas, pero mirando
algunas páginas me he dado cuenta de que son más complejas de lo que parecen a
simple vista…
FRASES DE CELEBRIDADES MATEMÁTICAS.
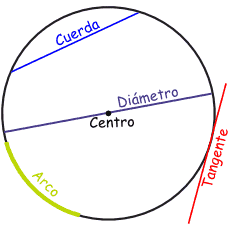
"En la circunferencia,
el comienzo y el fin coinciden."
Heráclito (544-480 a.
C.); filósofo griego
"Inútil es la labor del
que se fatiga intentando cuadrar el círculo."
Stiffel (1544)
"La naturaleza se
reduce a un número: p. Quien descubra el misterio de, comprenderá el
pensamiento de Dios..."
Isaac Newton
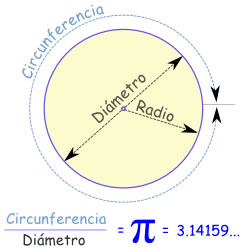
"El diámetro de un
circulo no mide a la circunferencia como un entero a un entero."
Johann Heinrich Lambert
(1728-1777).
"El rostro de p estaba
enmascarado; se sobreentendía que nadie podía contemplarlo y continuar con
vida. Pero unos ojos de penetrante mirada acechaban tras la máscara,
inexorables, fríos y enigmáticos."
Bertrand Russell,
Pesadillas de personas ilustres
"El matrimonio es un
poco como el número p: natural, irracional y muy importante"
Lisa Hoffman